[ad_1]
A Scholar’s t-distribution is nothing greater than a Gaussian distribution with heavier tails. In different phrases, we will say that the Gaussian distribution is a particular case of the Scholar’s t-distribution. The Gaussian distribution is outlined by the imply (μ) and the usual deviation (σ). The Scholar t distribution, however, provides a further parameter, the levels of freedom (df), which controls the “thickness” of the distribution. This parameter assigns larger chance to occasions farther from the imply. This characteristic is especially helpful for small pattern sizes, corresponding to in biomedicine, the place the belief of normality is questionable. Observe that because the levels of freedom improve, the Scholar t-distribution approaches the Gaussian distribution. We will visualize this utilizing density plots:
# Load mandatory libraries
library(ggplot2)# Set seed for reproducibility
set.seed(123)
# Outline the distributions
x <- seq(-4, 4, size.out = 200)
y_gaussian <- dnorm(x)
y_t3 <- dt(x, df = 3)
y_t10 <- dt(x, df = 10)
y_t30 <- dt(x, df = 30)
# Create an information body for plotting
df <- information.body(x, y_gaussian, y_t3, y_t10, y_t30)
# Plot the distributions
ggplot(df, aes(x)) +
geom_line(aes(y = y_gaussian, coloration = "Gaussian")) +
geom_line(aes(y = y_t3, coloration = "t, df=3")) +
geom_line(aes(y = y_t10, coloration = "t, df=10")) +
geom_line(aes(y = y_t30, coloration = "t, df=30")) +
labs(title = "Comparability of Gaussian and Scholar t-Distributions",
x = "Worth",
y = "Density") +
scale_color_manual(values = c("Gaussian" = "blue", "t, df=3" = "crimson", "t, df=10" = "inexperienced", "t, df=30" = "purple")) +
theme_classic()
Observe in Determine 1 that the hill across the imply will get smaller because the levels of freedom lower because of the chance mass going to the tails, that are thicker. This property is what provides the Scholar’s t-distribution a lowered sensitivity to outliers. For extra particulars on this matter, you possibly can test this weblog.
We load the required libraries:
library(ggplot2)
library(brms)
library(ggdist)
library(easystats)
library(dplyr)
library(tibble)
library(ghibli)
So, let’s skip information simulations and get critical. We’ll work with actual information I’ve acquired from mice performing the rotarod take a look at.
First, we load the dataset into the environment and set the corresponding issue ranges. The dataset accommodates IDs for the animals, a groping variable (Genotype), an indicator for 2 completely different days on which the take a look at was carried out (day), and completely different trials for a similar day. For this text, we mannequin solely one of many trials (Trial3). We are going to save the opposite trials for a future article on modeling variation.
As the information dealing with implies, our modeling technique will probably be primarily based on Genotype and Day as categorical predictors of the distribution of Trial3.
In biomedical science, categorical predictors, or grouping components, are extra frequent than steady predictors. Scientists on this discipline prefer to divide their samples into teams or circumstances and apply completely different therapies.
information <- learn.csv("Knowledge/Rotarod.csv")
information$Day <- issue(information$Day, ranges = c("1", "2"))
information$Genotype <- issue(information$Genotype, ranges = c("WT", "KO"))
head(information)
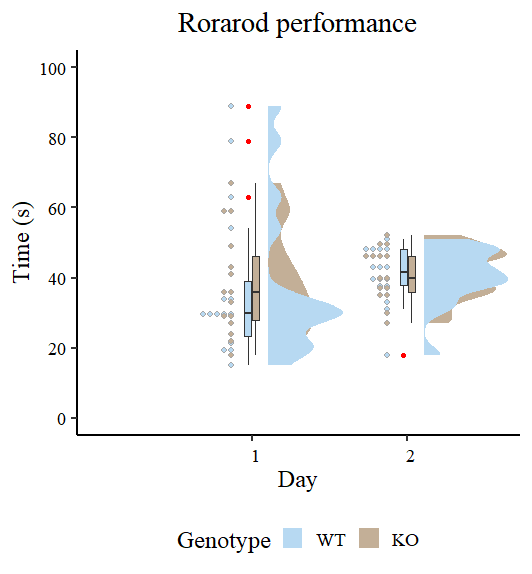
Let’s have an preliminary view of the information utilizing Raincloud plots as proven by Guilherme A. Franchi, PhD in this nice weblog submit.
edv <- ggplot(information, aes(x = Day, y = Trial3, fill=Genotype)) +
scale_fill_ghibli_d("SpiritedMedium", path = -1) +
geom_boxplot(width = 0.1,
outlier.coloration = "crimson") +
xlab('Day') +
ylab('Time (s)') +
ggtitle("Rorarod efficiency") +
theme_classic(base_size=18, base_family="serif")+
theme(textual content = element_text(dimension=18),
axis.textual content.x = element_text(angle=0, hjust=.1, vjust = 0.5, coloration = "black"),
axis.textual content.y = element_text(coloration = "black"),
plot.title = element_text(hjust = 0.5),
plot.subtitle = element_text(hjust = 0.5),
legend.place="backside")+
scale_y_continuous(breaks = seq(0, 100, by=20),
limits=c(0,100)) +
# Line beneath provides dot plots from {ggdist} package deal
stat_dots(facet = "left",
justification = 1.12,
binwidth = 1.9) +
# Line beneath provides half-violin from {ggdist} package deal
stat_halfeye(alter = .5,
width = .6,
justification = -.2,
.width = 0,
point_colour = NA)
edv
Determine 2 seems to be completely different from the unique by Guilherme A. Franchi, PhD as a result of we’re plotting two components as an alternative of 1. Nonetheless, the character of the plot is similar. Take note of the crimson dots, these are those that may be thought-about excessive observations that tilt the measures of central tendency (particularly the imply) towards one path. We additionally observe that the variances are completely different, so modeling additionally sigma may give higher estimates. Our process now’s to mannequin the output utilizing the brms package deal.
[ad_2]